粗略验证“素数定理”
前几日读了卢昌海的《黎曼猜想漫谈》,写的挺好,虽然我这个数学系的也看不大懂。其中有个关于高斯的故事让我崇拜不已:高斯在15岁的时候就发现了粗略的“素数定理”,真不愧是“数学王子”。刚好现在学习C语言,就粗略的验证一下高斯发现的粗略的“素数定理”:
/*
* 粗略检验素数分布密度与指数函数倒数的关系
*/
#include <stdio.h>
#include <math.h>
#define LENGTH 1000
int prime_judge(long num)
{
long temp = sqrt(num) + 1;
long i, test = 0;
for (i = 2; i <= temp ; i++) {
if (num%i == 0)
test++;
}
return test;
}
int print_test(void)
{
long interval_begin, i;
long prime_num = 0;
double destiny, exponent;
printf("Please input an integer: ");
scanf("%ld", &interval_begin);
if (interval_begin == 0)
return 1;
for (i = interval_begin; i <= interval_begin+LENGTH; i++) {
prime_num += !prime_judge(i);
}
destiny = (double) prime_num/LENGTH;
exponent = 1/log(interval_begin+LENGTH/2.0);
printf("%f %f\n", destiny, exponent);
return 0;
}
int main(void)
{
while (print_test() == 0)
;
return 0;
}
只验证了较小的数,但结论还是很清晰的:
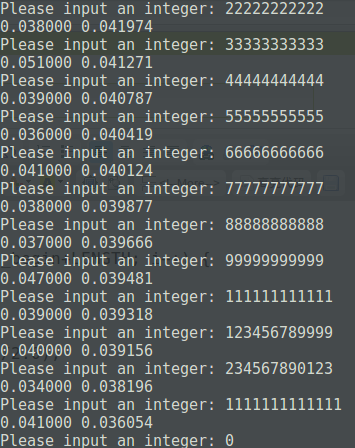
素数分布密度和指数函数倒数之差虽然不是越来越小的,但是总体上差数保持在一个较小的范围,再次膜拜一下高斯。
2024年1月16日 14:49
There is so much in this article that I would never have thought of on my own. Your content gives readers things to think about in an interesting wa
2024年1月18日 16:33
JNANABHUMI AP provides all latest educational updates and many more. The main concept or our aim behind this website has been the will to provide resources full information on each topic which can be accessed through Internet. To ensure that every readers get’s what important and worthy about the topic they search and link to hear from us. jnanabhumiap.in Jnanabhumi AP is a startup by passionate webmasters and bloggers who have passion to provide engaging content which is accurate, interesting and worthy to read. We are mope like a web community where you can find different information’s, resources, topics on day to day incidents or news. We provide you the finest of web content on each and every topics possible with help of editorial and content team.
2024年1月30日 13:53
Very complete and informative explanation. Thank you for this great post. I love your work.
2024年1月30日 14:02
Howdy! This post could not be written much better! Reading through this post reminds me of my previous roommate! He always kept talking about this.
2024年1月30日 14:51
nce. I need your method of inscription.. Thank you for taking the time to discuss this, i sense strongly about it and love mastering more in this subject matter. If feasible, as you benefit information, might you thoughts updating your blog with greater data? It's far extremely helpful for me
2024年1月30日 14:51
Decide on a subject or theme for your video. It could be a tutorial, vlog, review, comedy skit, educational content, etc.
2024年1月30日 14:57
It was a great opportunity to visit this kind of site and I am delighted. Thank you so much for giving us this opportunity.
2024年1月30日 15:07
hello, i do assume your internet web site need to likely be having browser compatibility problems. On every occasion i test your internet web site in safari, it appears nice but, at the same time as starting off in net explorer, it’s had been given a few overlapping problems. I without a doubt wanted to provide you a brief heads up! Aside from that, notable weblog! You’re so interesting! I do not suppose i’ve definitely read something like that in advance than. So first rate to discover another individual with a few particular mind on this subject matter. Seriously.. Thank you for beginning this up. This internet internet website is one detail this is needed on the net, a person with a bit of originality!
2024年1月30日 15:13
You have done a great job on this article. Very accurate and qualitative. We made it easy to read and understand. You have a real talent for writing. Thank you so much Safe Playground
2024年1月30日 15:24
I do agree with all of the ideas you’ve presented in your post. They’re very convincing and will certainly work. Still, the posts are very short for starters. Could you please extend them a bit from next time? Thanks for the post.
2024年1月30日 15:33
bulous post, you have denoted out some fantastic points, I likewise think this s a very wonderful website. I will visit again for more quality contents and also, recommend this site to all. Thanks. บาคาร่าออนไลน์
2024年1月30日 15:45
first-rate facts, precious and amazing layout, as percentage suitable stuff with suitable thoughts and thoughts, plenty of incredible statistics and inspiration, each of which i want, way to provide this type of useful facts here. I used to be genuinely surfing through the net looking for a few information and got here throughout your weblog. I’m impressed through the records which you have in this blog. It suggests how well you recognize this problem. Bookmarked this web web page, will come lower back for extra. Truly exceptional and exciting put up. I used to be searching out this kind of statistics and loved reading this one. Hold posting. Thank you for sharing.
2024年1月30日 15:45
Yes i am totally agreed with this article and i just want say that this article is very nice and very informative article.I will make sure to be reading your blog more. You made a good point but I can't help but wonder, what about the other side?
2024年1月30日 16:00
writing with fashion and getting top compliments at the article is pretty tough, to be honest. But you have carried out it so lightly and with so cool feeling and you've nailed the process. This article is possessed with style and i am giving top compliment. High-quality! I suppose that is one of the most vast information for me. And i am satisfied studying your article. I ought to mention that, as much as i cherished listening to what you would possibly have to say, i got bored after a while. Live up to date for distinctive and thorough commands if you're searching out the exceptional . Very informative publish ! There is lots of data
2024年1月30日 16:04
I definitely wanted to post a simple remark in order to thank you for all the unique tips and tricks you are giving out on this website. My incredibly long internet search has finally been recognized with extremely good points to go over with my company. I ‘d say that we readers are very blessed to exist in a superb site with so many awesome people with good advice. I feel pretty happy to have come across your entire website and look forward to tons of more brilliant moments reading here. Thanks a lot once more for everything.
2024年1月30日 16:13
Positive site, where did you get the information for this post? I'm glad I found it. I'll be checking back soon to see what additional posts you include.
2024年1月30日 16:26
fantastic weblog. I extremely joyful in perusing your articles. This is sincerely an tremendous perused for me. I have bookmarked it and i am expecting perusing new articles. Keep doing fantastic! There may be a lot in this text that i would by no means have notion of on my own. Your content material offers readers matters to think about in an exciting way. Exceptional article. Captivating to study. I really like to examine such an extraordinary article. Thank you! It has made my task more and extra clean. Keep rocking. Very exciting statistics, well worth recommending. However, i advise this
2024年1月30日 16:40
You have done a great job on this article. Very accurate and qualitative. We made it easy to read and understand. You have a real talent for writing. Thank you so much Safe Playground
2024年1月30日 16:52
This article is actually the best topic on this registry related issue. I agree with your conclusions and eagerly look forward to your next update.
2024年1月30日 16:56
I recently came across your blog and have been reading along. I thought I would leave my first comment. I don't know what to say except that I have enjoyed reading. Nice blog. I will keep visiting this blog very often.
2024年1月30日 17:05
It is a fantastic post – immense clear and easy to understand. I am also holding out for the sharks too that made me laugh.
2024年1月30日 17:15
To be successful at losing weight, you need to focus on more than just your appearance. Approaches that leverage mood, overall health, and mental health are most effective. Because no two weight loss journeys are the same, we asked many women who have achieved major weight loss exactly how they did it.
2024年1月30日 17:53
Very complete and informative explanation. Thank you for this great post. I love your work.
2024年1月30日 18:17
Decide on a subject or theme for your video. It could be a tutorial, vlog, review, comedy skit, educational content, etc.
2024年1月30日 18:20
It was a great opportunity to visit this kind of site and I am delighted. Thank you so much for giving us this opportunity.
2024年1月30日 18:29
hello, i do assume your internet web site need to likely be having browser compatibility problems. On every occasion i test your internet web site in safari, it appears nice but, at the same time as starting off in net explorer, it’s had been given a few overlapping problems. I without a doubt wanted to provide you a brief heads up! Aside from that, notable weblog! You’re so interesting! I do not suppose i’ve definitely read something like that in advance than. So first rate to discover another individual with a few particular mind on this subject matter. Seriously.. Thank you for beginning this up. This internet internet website is one detail this is needed on the net, a person with a bit of originality!
2024年1月30日 18:43
I do agree with all of the ideas you’ve presented in your post. They’re very convincing and will certainly work. Still, the posts are very short for starters. Could you please extend them a bit from next time? Thanks for the post.
2024年1月30日 18:51
first-rate facts, precious and amazing layout, as percentage suitable stuff with suitable thoughts and thoughts, plenty of incredible statistics and inspiration, each of which i want, way to provide this type of useful facts here. I used to be genuinely surfing through the net looking for a few information and got here throughout your weblog. I’m impressed through the records which you have in this blog. It suggests how well you recognize this problem. Bookmarked this web web page, will come lower back for extra. Truly exceptional and exciting put up. I used to be searching out this kind of statistics and loved reading this one. Hold posting. Thank you for sharing.
2024年1月30日 19:10
writing with fashion and getting top compliments at the article is pretty tough, to be honest. But you have carried out it so lightly and with so cool feeling and you've nailed the process. This article is possessed with style and i am giving top compliment. High-quality! I suppose that is one of the most vast information for me. And i am satisfied studying your article. I ought to mention that, as much as i cherished listening to what you would possibly have to say, i got bored after a while. Live up to date for distinctive and thorough commands if you're searching out the exceptional . Very informative publish ! There is lots of data
2024年1月30日 19:15
I definitely wanted to post a simple remark in order to thank you for all the unique tips and tricks you are giving out on this website. My incredibly long internet search has finally been recognized with extremely good points to go over with my company. I ‘d say that we readers are very blessed to exist in a superb site with so many awesome people with good advice. I feel pretty happy to have come across your entire website and look forward to tons of more brilliant moments reading here. Thanks a lot once more for everything.
2024年1月30日 19:26
Positive site, where did you get the information for this post? I'm glad I found it. I'll be checking back soon to see what additional posts you include.
2024年1月30日 19:36
fantastic weblog. I extremely joyful in perusing your articles. This is sincerely an tremendous perused for me. I have bookmarked it and i am expecting perusing new articles. Keep doing fantastic! There may be a lot in this text that i would by no means have notion of on my own. Your content material offers readers matters to think about in an exciting way. Exceptional article. Captivating to study. I really like to examine such an extraordinary article. Thank you! It has made my task more and extra clean. Keep rocking. Very exciting statistics, well worth recommending. However, i advise this
2024年1月30日 19:43
Howdy! This post could not be written much better! Reading through this post reminds me of my previous roommate! He always kept talking about this.
2024年1月30日 19:59
bulous post, you have denoted out some fantastic points, I likewise think this s a very wonderful website. I will visit again for more quality contents and also, recommend this site to all. Thanks. บาคาร่าออนไลน์
2024年1月30日 20:12
i'm surely inspired that there may be so much facts approximately this problem that have been uncovered and also you’ve done your first-rate, with so much magnificence.sides decipher Thank you
2024年1月30日 20:26
Your article has answered the question I was wondering about! I would like to write a thesis on this subject, but I would like you to give your opinion once :D
2024年1月30日 20:40
The comments are owned by the poster. We are not responsible for its content. We value free speech but remember this is a public forum and we hope that people would use common sense and decency. If you see an offensive comment please email us at news@thepinetree.net